Calibration of the NVP_i

Two levels of calibration are necessary in appropriately calibrating an Ion-Selective Vibrating Probe, NVP_i.

• First, it must be correctly calibrated in a stationary mode.
• Second, it must be calibrated in the more dynamic oscillating mode.

Stationary mode calibration must be performed at some level on every electrode that is used.   Dynamic calibration should be done at least once for each LIX and sampling protocol.   It is particularly sensitive to LIX column length, oscillation frequency, electrode shape, stepper motor speed, and interfering ions.

Stationary Calibration:
In the stationary mode, the electrode is calibrated as if it were an ordinary ion selective electrode using methodology similar to a laboratory pH meter.   One places the electrode into a series of carefully made standard solutions of the ion of interest and determines the mV response after the electrode has come to rest for a suitable time.   This stage should establish the range in which the electrode gives a linear response and how close that response complies to the Nernst Equation.   An electrode at this stage of calibration will be described as 'Nernstian' if it has a slope [mV vs log₁₀ concentration] which is close to the expected (58 mV for a monovalent cation and 29 mV for a divalent cation).   For most LIXs our experience is that the slopes approach to Nernstian is more a function of the care in preparing the standards than most other factors.   Thus, if an electrode is giving you a close but non-exactly Nernstian slope, suspect the standards first.   If systematicly non-Nernstian electrodes are being obtained, suspect in order, linear range of the LIX, ground electrode, electrode tip size, loss of LIX from poorly silanized electrode glass, temperature of measurement.   You must establish confidence that your electrodes are performing like a good pH meter measuring proton concentration.   When one has such confidence, a broken electrode can be quickly replace with a new one, applying a one-point calibration in the physiological saline being used for the experiment.

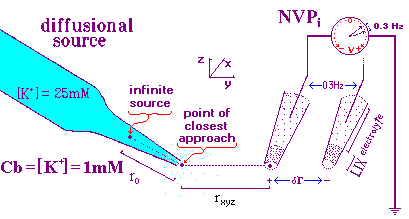
An artificial source for dynamic calibration:
The use of a capilary tube with a finely drawn tip as an artificial source of flowing ions was established by the developers of the technique (Kühtreiber and Jaffe, 1990).   This source provides a concentration gradient eminating from its tip that in an undisturbed setting with minimal convection is inversely related to the distance from the tip to the point of measurement, approaching with slope K the background concentration, Cb, at infinite radius, r, when 1/r = zero.   To the extent this voltage/inverse-distance curve is linear, the µV difference associated with a change in radius is predictable, using the assumptions of linearity and the slope and intercept of that line.   This situation provides a physically predictable model about which one can predict the expected µV drop over a specified distance as well as a physical model in which actual measurements could be made.   From the difference between the predicted and actual measurements one can calculate an efficiency of the measurement process.

µV Calibration during Oscillation (dynamic calibration):
The movement of the electrode during the µV difference measurement places special demands on the calibration process.   The speed with which the LIX in the electrode can respond to the changed concentration after the move varies with the LIX used as well as the geometry of the electrode.   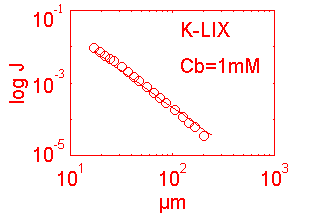In addition, one needs to use an artificial source from which one can predict an expected flux of the ion of interest; and on which one can determine the efficiency of the dynamic measuring process.   Fig 1, below presents a cartoon of the dynamic calibration setup.

Fig 1.   Model of a Diffusional Point Source and a NVP_i

This model was constructed for the calibration of ion probes using the 3DVIS software package in which the electrode is continuously oscillating (0.3 Hz in this example).   The more advanced software, ASET, is based on a discrete movement sampling rule approach which eliminates the continuous oscillation and demands a different calibration protocol. The two protocols for 3DVIS and ASET will be explained separately.   The two protocols share the following features illustrated in Fig 1.  

• Electrode Construction.
• Ground Construction.
• Artificial Diffusional Source Geometry.
• XYZ Spatial Geometry.
• Oscillation, dr.
• Direct Coupled Measurement of Voltage (Applicable Electronics)
  (beware that capacitatively coupled amplifier probe systems may not effectively be calibrated with these protocols.)

Fig 2.   Predicted and observed µVolt difference curves for diffusion of protons (left) and potassium (right) from a point source:

Predictive equation for dV, the µV difference at a point in space, r µ from a point source:

                                       eff = efficiency of the measure
         S K dr                          r = distance to point source
dV = eff ------- / (Cb + K/r),  where:  dr = oscillation distance
          z r2                           K = slope of [ion] curve
                                        Cb = background [ion]
                                         S = Nernst coeficient
                                         z = unit charge on the ion

This calibration curve allows one to estimate the efficiency, eff, of the electrode which can be used to turn any µV difference measured with a similar electrode into an observed flux of that ion in the space arround a cell or tissue.

Fig 3.   Ion flux, J, emanating from a distant (µm) point source:
Observed and predicted values for 2 LIXs, proton (left) and potassium (right).

Predictive equation for ionic flux, J_o:

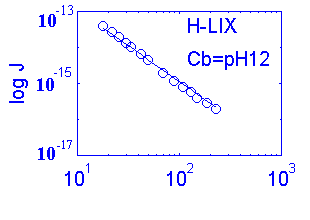
                              D = diffusion coeficient for the ion (cm-2 sec-1)
  Jo  =  - D dC/dr ,  where  dC = concentration differential
                             dr = oscillation differential

Calibration Using 3DVIS Software
Ion	Do	i	Nernst slope	LIX	t90	Hz	eff%
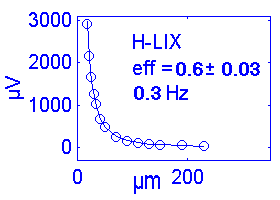
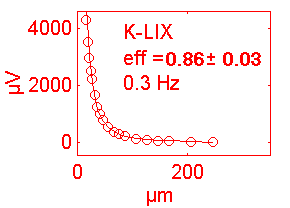
K+	19.6	+1	58	K IB	<1s.	0.3	70%
H+	93.7	+1	58	H IIA	~0.6s	0.3	80%
Ca++	7.9	+2	29	Ca IIA	<5s	0.3	50%
Mg++	7.1	+2	29	Mg IV	<30s	0.25	30%
Cl-	-20.3	-1	-58
Calibration Using ASET Software

D is expressed as 10⁶D/cm² sec^-1.
Nernst Slope, S, is expressed in mV.

If you have questions about calibrating the various vibrating probes or the University of Massachusetts Vibrating Probe Facility, email its PI, Joe Kunkel