 |
 |
Forming a Parabolic dish with
cardboard segments
Scientific American- The Amateur Scientist
December 1973 page 126
(correction in Feb 1974 issue)
This is a design for a large cardboard parabolic reflector that could be used to focus sound onto a microphone. The method was presented in Scientific American by Alex McEachern and Paul Boon. I built a version of it in 1995 and mounted it on a base of my own design.
 |
 |
The units were originally in inches but they can be interpreted as any unit.
| Radius | R= | 27 | ||||
| No. of Sections | N= | 12 | ||||
| Focus | f= | 12 | ||||
| a= | 0.0208 | |||||
| Base of Triangle | B= | 17.37 | ||||
| Row | X | Y | Y1 | Z | Vd | D |
| 1 | 3 | 0.19 | 0.75 | 3.05 | 3.05 | 0.01 |
| 2 | 6 | 0.75 | 1.69 | 3.14 | 6.20 | 0.05 |
| 3 | 9 | 1.69 | 3.00 | 3.27 | 9.47 | 0.12 |
| 4 | 12 | 3.00 | 4.69 | 3.44 | 12.91 | 0.24 |
| 5 | 15 | 4.69 | 6.75 | 3.64 | 16.55 | 0.41 |
| 6 | 18 | 6.75 | 9.19 | 3.87 | 20.42 | 0.63 |
| 7 | 21 | 9.19 | 12.00 | 4.11 | 24.53 | 0.92 |
| 8 | 24 | 12.00 | 15.19 | 4.38 | 28.91 | 1.28 |
| 9 | 27 | 15.19 | 18.75 | 4.66 | 33.56 | 1.72 |
| 10 | 30 | 18.75 |
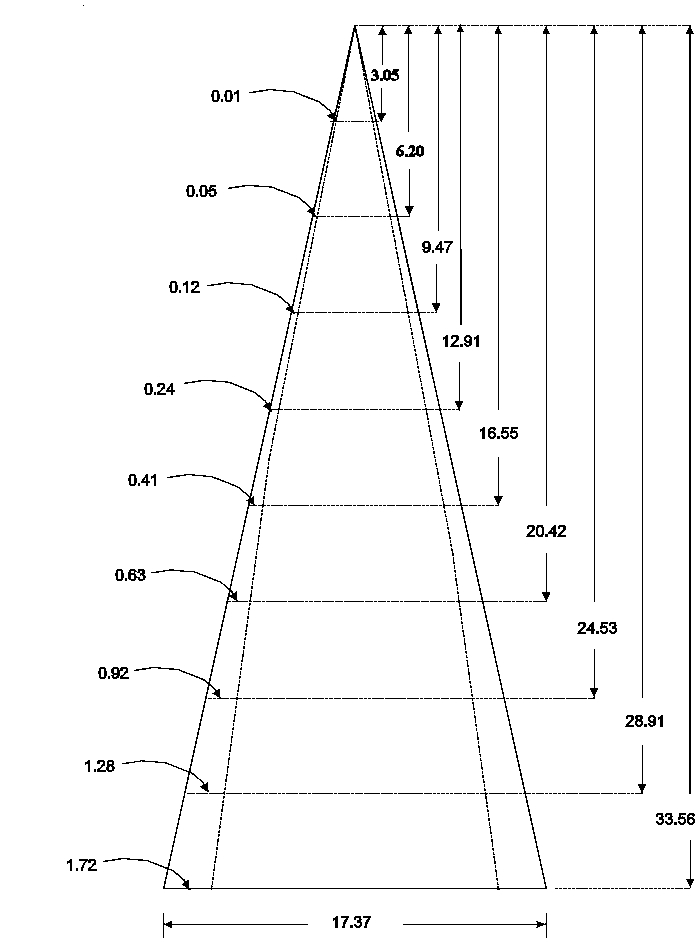
Steps in creating one section of the paraboloid.(54 inches wide with a focal length of 12 inches)
Draw an isosceles triangle with a height of 33.56 inches and base of 17.37 inches
To determine how much to trim each side of the
triangle (dashed lines above) draw trim line through the following
points from each edge:
at 3.05 inches down from the apex plot a point 0.01 inches in from each
edge
at 6.02 inches down from the apex plot a point 0.05 inches from each
edge
at 9.47 inches down form the apex plot a point 0.12 inches from each
edge
etc.
Continue this until you reach row 9
Connect these plotted points with a straight edge
Cut out section along trim line and base.
Using first section as a pattern trace out 11 more sections and cut them out
Construct paraboloid by gluing the edges of the sectors together. I used hot glue.
A spreadsheet to modify the above calculations that I programmed before I built the dish.
A diagram of the mount that I finally built.
References:
Paraboloids. how to construct: cardboard type,
1973 Dec, pg 122
Paraboloids. how to construct: fibreglass type,
1974 Nov, pg 126